RoPE

1 RoPE

旋转位置编码（Rotary Position Embedding, RoPE）是一种位置编码方法，广泛应用于 Transformer 架构中。它的核心思想是：

对输入向量的施加一个与位置相关的旋转变换，从而在注意力计算中，使得点积的结果中包含位置的相对差值 $n - m$ 信息

理论推导： Transformer升级之路：2、博采众长的旋转式位置编码 - 科学空间|Scientific Spaces
实现：

q 对应隐藏层的向量；d 是隐藏层维度，会是 512，768……；m 对应 token 在序列中位置
实际应用中常采用指数式分布： $θ_{j} = 10000^{- 2 j / d}$ ，以覆盖长短程不同的位置信息。
代码：

    def sinusoidal_pos_embed(self, seq_len, dim):
        """
        @return: (1, n, seq_len, dim) 完整的位置编码
        """
        inv_freq = 1.0 / (10000 ** (torch.arange(0, dim, 2).float() / dim))
        pos = torch.arange(seq_len, dtype = torch.float)
        # will product
        sinusoid_inp = torch.einsum("i,j->ij", pos, inv_freq)

        sinusoid_pos = torch.stack([sinusoid_inp.sin(), sinusoid_inp.cos()], dim = -1).reshape(seq_len, -1)
        sinusoid_pos = sinusoid_pos.unsqueeze(0).unsqueeze(0)

        return sinusoid_pos.repeat(1, self.n, 1, 1)

    def apply_RoPE(self, x, pos_id=0):
        seq_len = x.shape[2]
        pos_emb = self.sinusoidal_pos_embed[:, :, pos_id:pos_id + seq_len, :]
        # cos_pos,sin_pos: (bs, head, max_len, output_dim)
        # 看rope公式可知，相邻cos，sin之间是相同的，所以复制一遍。如(1,2,3)变成(1,1,2,2,3,3)
        pos_emb = pos_emb.to(x.device)
        # 将奇数列信息抽取出来也就是cos 拿出来并复制
        cos_pos = pos_emb[..., 1::2].repeat_interleave(2, dim = -1)
        # 将偶数列信息抽取出来也就是sin 拿出来并复制
        sin_pos = pos_emb[..., ::2].repeat_interleave(2, dim = -1)

        x2 = torch.stack([-x[..., 1::2], x[..., ::2]], dim = -1)
        # reshape后就是正负交替了
        x2 = x2.reshape(x.shape)

        x = x * cos_pos + x2 * sin_pos
        return x

探讨：

外推支持非常好，因为旋转变换的角度支持

2 数学形式

二维向量

Pasted image 20251004202138.png
（这里的 q 0，q 1实际上是实现中 q的 dim 隐藏层维度的 d1, d2）

给定输入向量的某个二维子空间：

q_{j}, k_{j} \in R^{2}

在位置 $m$ 的旋转矩阵为：

R_{j} (m) = (\begin{matrix} \cos (m θ_{j}) & - \sin (m θ_{j}) \\ \sin (m θ_{j}) & \cos (m θ_{j}) \end{matrix})

其中， $θ_{j}$ 为该子空间的角度步长，或者叫旋转的幅角，例如 $\frac{π}{50}$ 。m 为位置，例如序列的第0……100，实践上我们设置 $θ_{j}$ 为 $10000^{- 2 i / d}$ , $i = 1, 2, 3, 4 \dots \dots d / 2$ ，d 是隐藏层维度，例如 768。

旋转后的 Query/Key：

{\tilde{q}}_{m} = R_{j} (m) q_{j}, {\tilde{k}}_{n} = R_{j} (n) k_{j}

旋转后的 Query/Key 内积如下，嵌入了相对位置信息：

{\tilde{q}}_{m}^{⊤} {\tilde{k}}_{n} = q_{j}^{⊤} R_{j} (n - m) k_{j}

注意：以上的过程固定了幅角

多维向量

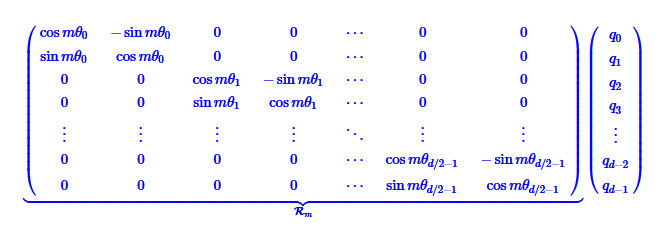
将 $d$ 维向量分为 $d / 2$ 个二维子空间，整体旋转矩阵为块对角矩阵：

T (m) = blockdiag (R_{0} (m), R_{1} (m), \dots, R_{d / 2 - 1} (m))

整体编码：

{\tilde{q}}_{m} = T (m) q, {\tilde{k}}_{n} = T (n) k

内积如下，只依赖相对位置：

{\tilde{q}}_{m}^{⊤} {\tilde{k}}_{n} = \sum_{j = 0}^{d / 2 - 1} q_{j}^{⊤} R_{j} (n - m) k_{j}

注意：这意味着，对于不同位置的 token，例如 len 1, len 2 位置的(对应于 n，m)，它们对应的向量进行内积，d 1，d 2 维度的幅角相同(q 0, q 1)，d 3，d 4 维度(q 2, q 3)的幅角相同，……, 也就是两两分组包括了相对位置信息在其中

2.1 推导

2.1.1 事后精简版

证明引入复数的幅角，即旋转矩阵，可以使得内积的结果包含了相对位置信息。

我们将二维向量 $(x, y)$ 看作复数 $z = x + i y$ 。在位置 $m$ 的旋转变换等价于乘以相位：

z \mapsto z e^{i m θ} .

于是两个位置 $m, n$ 的向量在内积中表现为：

Re (z_{q} e^{i m θ} \cdot (z_{k} e^{i n θ})^{*}) = Re (z_{q} z_{k}^{* e^{i (m - n) θ})}

显然只依赖于 $m - n$ ，而不是 m，n。

2.1.2 作者思路版

Transformer升级之路：2、博采众长的旋转式位置编码 - 科学空间|Scientific Spaces

作者首先假定运算 $f$ , 给 $q$ 和 $k$ 添加绝对位置信息，即

\begin{matrix} (1) & {\tilde{q}}_{m} = f (q, m), {\tilde{k}}_{n} = f (k, n) \end{matrix}

同时也自然有

\begin{matrix} (2) & f (q, 0) = q, f (k, 0) = k \end{matrix}

因为 $a t t e n t i o n$ 就是在做内积，所以假设其内积为 g，与 m - n 有关是希望它和相对位置有关，能反映它，这是我们的目标

\begin{matrix} (3) & ⟨ f (q, m), f (k, n) ⟩ = g (q, k, m - n) \end{matrix}

考虑 $f (q, m)$ 和 $f (k, m)$ 是复数进行求解，因为 $⟨ q, k ⟩ = Re [q k^{*}]$ ， $R e$ 代表实部，所以有

\begin{matrix} (4) & Re [f (q, m) f^{*} (k, n)] = g (q, k, m - n) \end{matrix}

这里作者为了简便，直接令

\begin{matrix} (5) & f (q, m) f^{*} (k, n) = g (q, k, m - n) \end{matrix}

性质奇妙的地方来了，作者考虑以复数指数的形式进行求解（任何一个复数都可以用指数形式表示），将 $f (q, m), f (k, m)$ 和 $g (q, k, m - n)$ 都以复数指数进行表达，有

\begin{matrix} (6) & \begin{aligned} f (q, m) & = R_{f} (q, m) e^{i Θ_{f} (q, m)} \\ f (k, n) & = R_{f} (k, n) e^{i Θ_{f} (k, n)} \\ g (q, k, m - n) & = R_{g} (q, k, m - n) e^{i Θ_{g} (q, k, m - n)} \end{aligned} \end{matrix}

其中， $R$ 表示实部， $Θ$ 表示虚部函数

因为 (5) 式的直接相等，所以实部等于实部，虚部等于虚部，注意（5）式的*表示共轭取反，因此有

\begin{matrix} (7) & \begin{aligned} R_{f} (q, m) R_{f} (k, n) & = R_{g} (q, k, m - n) \\ Θ_{f} (q, m) - Θ_{f} (k, n) & = Θ_{g} (q, k, m - n) \end{aligned} \end{matrix}

令 m = n = 0, (7)-1 有

R_{f} (q, 0) R_{f} (k, 0) = R_{g} (q, k, 0)

令 m = n，（7）-1 有

R_{f} (q, m) R_{f} (k, m) = R_{g} (q, k, m - n) = R_{g} (q, k, 0) = R_{f} (q, 0) R_{f} (k, 0)

注意到（2）式，所以

R_{f} (q, 0) R_{f} (k, 0) = R (q) R (k) = | | q | | * | | k | |

也即

R_{f} (q, m) R_{f} (k, m) = | | q | | * | | k | |

这说明两者的实部与 m 无关，也就是和位置无关，我们可以不关注这一项了

现在我们来看 (7)-2 式，令 m = n = 0, (7)-2 有

Θ_{f} (q, 0) - Θ_{f} (k, 0) = Θ_{g} (q, k, 0)

令 m = n，（7）-2 有

Θ_{f} (q, m) - Θ_{f} (k, m) = Θ_{g} (q, k, 0) = Θ_{f} (q, 0) - Θ_{f} (k, 0)

注意到（2）式，所以

Θ_{f} (q, 0) - Θ_{f} (k, 0) = Θ (q) - Θ (k)

也就是

Θ_{f} (q, m) - Θ_{f} (k, m) = Θ (q) - Θ (k)

因此

Θ_{f} (q, m) - Θ (q) = Θ_{f} (k, m) - Θ (k)

这意味着 $Θ_{f} (q, m) - Θ (q)$ 是一个只与 $m$ 有关，和 $q$ 无关的函数，记为 $φ (m)$ , 所以

\begin{matrix} (8) & Θ_{f} (q, m) = Θ (q) + φ (m) \end{matrix}

代入 $n = m - 1$ , 有

\begin{matrix} (9) & Θ_{f (k, m - 1)} = Θ_{f (k)} + φ (m - 1) \end{matrix}

由（7）（8）（9）式整理可得：

φ (m) - φ (m - 1) = Θ_{f} (q, m) - Θ (q) - Θ_{f (k, m - 1)} + Θ_{f (k)} = Θ_{f (q, k, 1)} + Θ_{f (k)} - Θ (q)

注意到等式的右边全部和 m 无关，可以认为是一个和 q, k 相关的常数，这意味着 $φ$ 是一个等差数列，令右端为 $θ$ , 有

φ (m) = m θ