Diffusion Models

1 简介

扩散模型（Diffusion Model），基本思想是模拟一个非平衡的热力学系统，通过逐步向数据中添加噪声（扩散过程）来逐渐破坏数据的结构，使数据点的分布在时间演化下逐渐趋于一个简单的高斯分布，然后再学习如何从噪声中重建原始数据的概率分布（反向扩散过程）。

物理学向下游学科的传播

因此，扩散模型并不具体指某种模型，而是一种范式。其基模型包括UNet、Transformer、ControlNet、GCN、GNN等。

UNet: 图像分割、编码-解码的U型结构、特征融合机制（跳跃连接）

GCN: 图卷积网络，分子设计

扩散模型大体上超越了GANs，在许多应用中具有破纪录的性能，包括CV、NLP、时间数据建模、多模态建模、鲁棒性机器学习（噪声、异常值或数据分布变化）、分子设计。

2 理论

三种理解角度

三种角度理解扩散模型：马尔科夫链过程、随机微分过程和基于分数的扩散过程。

2.1 马尔科夫链过程

原始论文：[2006.11239] Denoising Diffusion Probabilistic Models，

其以精心设计的扩散数学形式，从一步一步加噪、去噪角度，推导模型扩散过程的采样和训练过程。结论如下：

L o s s : M S E (N o i s e, N o i s e_{θ})

局限：

生成时，需要一步一步去噪（T = 500+），慢且开销大
因为时间步的离散，该过程离散。

2.1.1 详细推导

涉及的数学知识点：

高斯分布的重参数化技巧和可叠加性质
三元贝叶斯公式
最大化似然函数
连续数学期望
Jensen不等式
下界函数

详细推导过程此处略，可参考个人手稿：DDPM数学推导

马尔科夫链过程，是理解扩散模型系列的基础

顺带理解VAE的数学内核

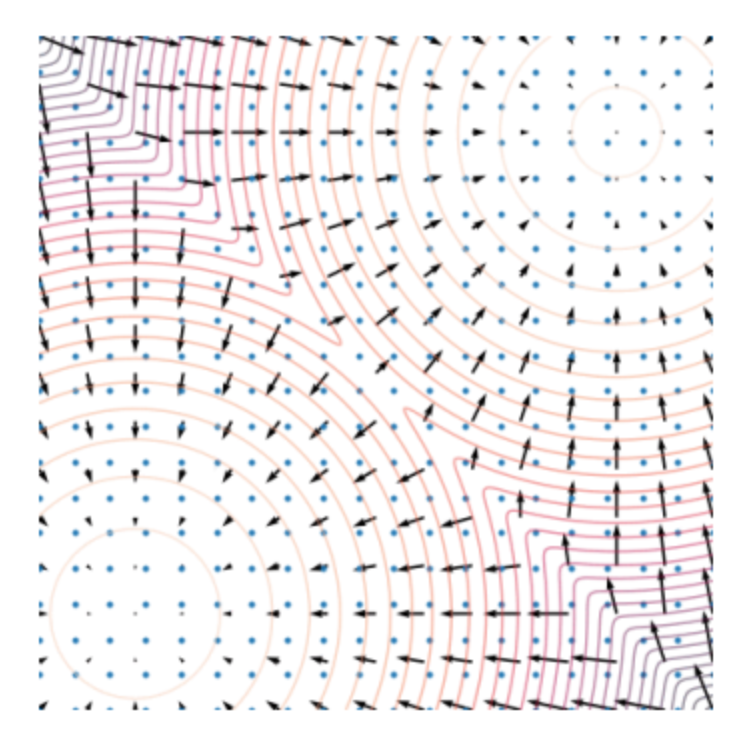
2.2 Score-Based Diffusion

原始论文：

Estimation of Non-Normalized Statistical Models by Score Matching。分数匹配的开创性文章，2005年发表于Journal of Machine Learning Research，Cia-1500，提出分数匹配以解决参数化模型的常数项问题，并以最小化SE为目标函数，将该方法推向了离散、连续情况
[1907.05600] Generative Modeling by Estimating Gradients of the Data Distribution。分数匹配 + 扩散模型

意义：一种新视角去理解扩散模型。

2.2.1 背景

我们希望，能够重建真实的数据概率分布（概率密度函数 PDF），即式子1：

p (x; θ) = \frac{1}{Z (θ)} q (x; θ)

其中，p表示真实的数据概率分布，q表示某个未归一化的概率函数（原文：分析表达式）；Z表示归一化常数，使得 $\int p (x; θ) d x = 1$ 。

需要说明的是，Z是一个关于 $θ$ 的归一化常数，也就是说，它与数据本身无关，而与选择的模型有关，这是因为 Z(θ) 是通过对 q(x;θ) 在整个数据空间上进行积分来得到的，这个积分过程并不涉及具体的数据点，而是与 q(x;θ) 的形状和 θ 的取值有关。而由于 q(x;θ) 的形式是由我们选择的模型决定的（例如常见的正态分布假设），并且该模型中的参数为 θ，所以 Z(θ) 也就与 θ 有关。

根据极大似然，我们可以通过训练 $θ$ ，最大化观测数据的对数似然 $p_{θ} (x)$ 来拟合式子1，即式子2

max_{θ} \sum_{i = 1}^{N} \log p_{θ} (x_{i})

注意，此时我们的变量是 $θ$ , 也因此极大似然中会包括Z关于 $θ$ 的偏导。所以，为了计算 $p_{θ} (x)$ ，我们必须评估归一化常数 $Z_{θ}$ 。对于高维大量数据，这带来基本不现实的开销。

原始论文1表明，2005年，2维以上的数据计算该常数即不可行

2.2.2 对比

几种传统解决办法：

自回归模型中的因果卷积。确保了生成过程的顺序性，它使得模型能够逐步地、条件地生成数据，从而避免了计算整个联合概率分布的归一化常数。每个条件概率都是可处理的。
归一化流模型中的可逆网络。归一化流模型中的变换是可逆的，意味着存在一个从数据空间到潜在空间的映射，同时也存在一个相反的映射，即从潜在空间回到数据空间。可以通过变换方法，例如计算雅可比行列式，来调整概率密度，使得模型能够精确地计算经过一系列变换后 $Z_{θ}$ 的概率密度。
近似归一化常数。VAE 中的变分推理通过下界进行估计，或KL散度&MCMC 采样估计。下图说明了 p 存在时，引入 q 和变分上届，能够对进行式子 2 求解. 也就解决了所谓“归一化常数”（注意，VAE 推导没有这个，可以理解为此处的背景是更高的一种维度看法）

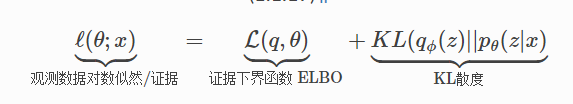
2.2.3 分数函数

通过对分数函数而不是密度函数进行建模，我们可以避免难以处理的归一化常数的困难。评分函数 $s_{θ} (x)$ 定义为

s_{θ} (x) = \nabla_{x} \log p (x; θ)

也就是概率密度函数 PDF的梯度。
可以令下式：

q (x; θ) = e^{- f_{θ} (x)}

计算可得：

s_{θ} (x) = \nabla_{x} \log p_{θ} (x) = - \nabla_{x} f_{θ} (x) - \underset{= 0}{\underset{⏟}{\nabla_{x} \log Z_{θ}}} = - \nabla_{x} f_{θ} (x) .

那么计算梯度是否可行呢？参数化模型对于观测数据 $x$ 梯度，能否引导模型正确地更新参数？具体又如何更新呢？这就引入了下面的采样过程。

2.2.3.1 采样过程

可以想到的是，这个梯度信息提供了，如何调整样本以使其更可能来自目标分布p(x)的指示。我们可以让样本沿着这个梯度变化，使其越来越接近真实分布的p(x)。

朗之万采样是一种基于梯度信息的MCMC（马尔可夫链蒙特卡洛）采样方法，它结合了随机梯度下降（SGD）和随机漫步的思想。在每次迭代中，它首先计算目标分布的对数概率密度的梯度，然后使用该梯度信息来更新样本，并添加一些随机噪声以保持遍历性。

具体过程如下：
先任意选择一个 $x_{0}$ , 然后重复:

求 $x_{t}$ 的梯度 $\nabla p (x_{t})$
更新样本： $ϵ$ 视作学习率, 梯度上升的过程中加 $\sqrt{2 ϵ}$ 倍的正态分布噪声。

x_{t + 1} = x_{t} + ϵ \nabla p (x_{t}) + \sqrt{2 ϵ} z_{i}, z_{i} \sim N (0, 1)

加入噪声是为了增大原始数据分布，因为我们的数据总是原始分布的一个子集。

一个例子：
加噪前
加噪后

2.2.3.2 训练目标函数

假设我们有变量 $x$ 的一些观测样本, 我们用 $p_{data} (x)$ 表示这些数据的真实分布, 然后定义一个近似的参数化分布（训练的模型）表示为 $p_{θ} (x)$ , 分数匹配的目标函数是

\begin{aligned} J (θ) & = \frac{1}{2} \int p_{data} (x) {‖ \nabla \log p_{data} (x) - \nabla \log p_{θ} (x) ‖}^{2} d x \\ = \frac{1}{2} E_{p_{data} (x)} [{‖ \nabla \log p_{data} (x) - \nabla \log p_{θ} (x) ‖}^{2}] \end{aligned}

为了符号简洁, 分别定义 $s_{θ} (x) = \nabla \log p_{θ} (x), s_{data} (x) = \nabla \log p_{data} (x)$ , 注意这里的梯度都是关于变量 $x$ 的, 而不是参数 $θ$ 。

\begin{aligned} J (θ) & = \frac{1}{2} \int p_{data} (x) {‖ s_{data} (x) - s_{θ} (x) ‖}_{2}^{2} d x \\ = \frac{1}{2} E_{p_{data} (x)} [{‖ s_{data} (x) - s_{θ} (x) ‖}_{2}^{2}] \end{aligned}

通过极小化目标函数求得参数化分布的未知参数

\hat{θ} = \underset{θ}{\arg min} J (θ)

2.3 SDE与DDPM

SDE: Stochastic Differential Equation，随机微分方程，其一般数学形式如下：

d X_{t} ​ = μ (X_{t} ​, t) d t + σ (X_{t} ​, t) d W_{t} ​

$μ (X_{t} , t)$ 表示漂移项，描述了系统在时间 $t$ 的位置 $X_{t}$ 处的确定性变化率
$σ (X_{t} , t)$ 表示扩散项，描述了系统在时间 $t$ 的位置 $X_{t}$ 处的随机变化率
$d X_{t}$ 表示 $X_{t}$ 随机过程在时间 $t$ 上的微小变化量
$d_{t}$ 表示微小的时间表达量
$d W_{t}$ 表示布朗运动的微小增量

Info

粒子的布朗运动是指在液体或气体中的微小颗粒由于受到介质分子的碰撞而表现出的随机运动。这种运动是由英国生物学家罗伯特·布朗在19世纪观察到的，他通过显微镜观察到颗粒在水中不规则地移动，这种移动是由于水分子不断碰撞颗粒而引起的。

具有以下特性：

独立性：布朗运动是马尔可夫过程，对于不同的时间间隔 s<t<u，增量 dWt和 dWs 是独立的。
正态性：根据中心极限定理，布朗运动的位置变化增量 dWt服从均值为零、方差为 dt的正态分布。

SDE表达一个扩散过程，相当于 DDPM 中的前向扩散过程，只不过在 DDPM 中，时间 𝑡 是离散的，而在SDE中，时间是连续的。因此 SDE 可以看做是DDPM在连续时间上的扩展 。

2.4 Score-Based SDE Diffusion

原始论文： [2011.13456] Score-Based Generative Modeling through Stochastic Differential Equations
意义：统一了两种视角，将扩散推向了连续并简化，为后续扩散模型的大统一框架打下基础，同时其中的SDE、Score-Based在后续工业界中被广泛使用。

2.4.1 内容

略。

2.5 基于条件的扩散模型

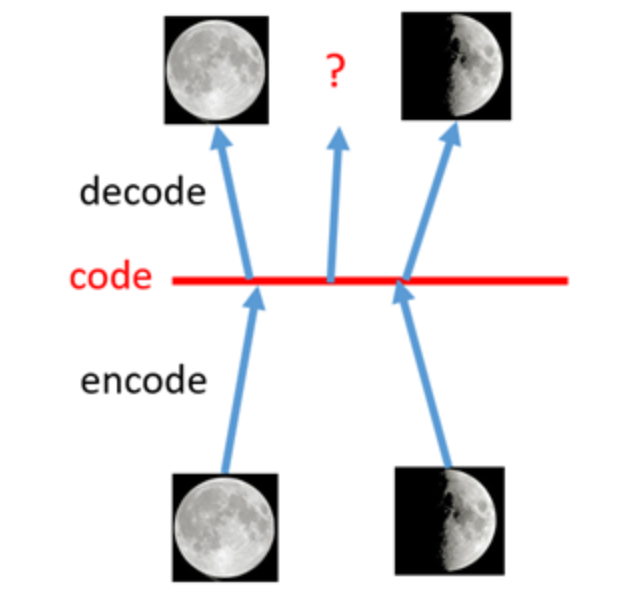
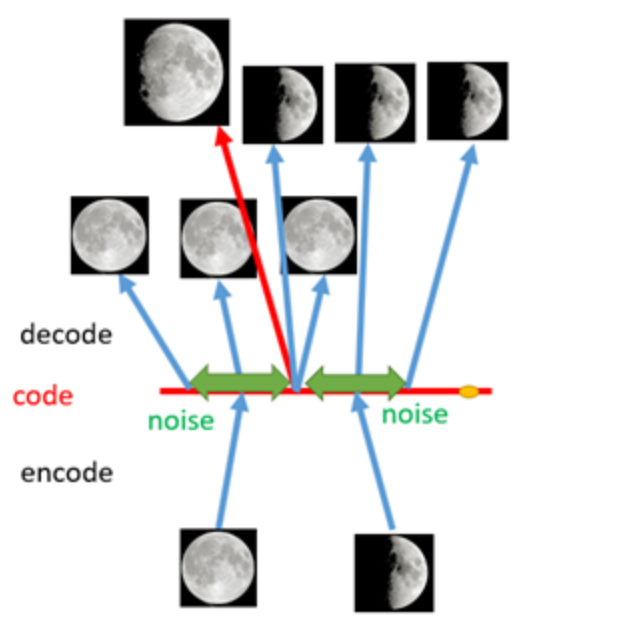
无论是 DDPM 还是 DDIM，这些扩散模型在生成图片时，都是轮入一个随机高斯噪声数据, 然后逐步的产出一张有意的真实图片。这个过程中每一步都是一个随机过程, 所以每次执行产出的图片都不一样, 生成的图像多样性非常好。但这也是一个缺点：生成的图像不控，无法控制这个生成过程并令其生成我们想要的图像内容。

假设这个额外的信息为 $y$ , 引入 $y$ 之后的模型就变成了一个以 $y$ 为条件的条件概率分布。

p (x_{1 : T} ∣ y, x_{0})

引入 y 之后，对前向扩散过程没有任何影响，也就是不影响加入噪声量和噪声分布，即

\hat{q} (x_{t} ∣ x_{t - 1}, y) := q (x_{t} ∣ x_{t - 1})

$\land$ 的符号表示引入 $y$ 之后，条件扩散模型中的概率分布，不带 $\land$ 符号表示原始（无条件）扩散模型的概率分布。

个人认为，引入 y可以影响前向扩散，因为一张纯色图片和一张五彩斑斓的图片，需要的前向扩散时间步，显然不同

2.5.1 classifier guidance

OpenAI 的团队在 2021 年发表一篇论文 Diffusion models beat gans on image synthesis ，这篇论文提出一种利用图片类别标签指导图像生成的方案，称为 classifier guidance。
推导过程如下：

式 子 1 \begin{aligned} \nabla_{x_{t}} \log p (x_{t} ∣ y) & = \nabla_{x_{t}} \log (\frac{p (x_{t}) p (y ∣ x_{t})}{p (y)}) \\ = \nabla_{x_{t}} \log p (x_{t}) + \nabla_{x_{t}} \log p (y ∣ x_{t}) - \underset{与 x_{t} 无夫, 为 0}{\underset{⏟}{\nabla_{x_{t}} \log p (y)}} \\ = \underset{unconditional score}{\underset{⏟}{\nabla_{x_{t}} \log p (x_{t})}} + \underset{adversarial gradient}{\underset{⏟}{\nabla_{x_{t}} \log p (y ∣ x_{t})}} \end{aligned}

显然, 条件扩散模型的分数项 $\nabla x_{t} \log p (x_{t} ∣ y)$ 就是在非条件扩散模型分数项 $\nabla x_{t} \log p (x_{t})$ 的基础上加了一项分类器的对抗梯度。
condition score $=$ unconditional score + adversarial gradient
这个分类器需要再训练条件扩散模型之前，独立的训练好。

训练过程：

为了能更灵活的控制生成内容的方向, 论文中增加了一个超参数 $λ$ , 作为一个权重项。显然这个权重可以调节类别引导的作用大小。

式 子 2 — — \begin{array}{r} \nabla_{x_{t}} \log p (x_{t} ∣ y) = \nabla_{x_{t}} \log p (x_{t}) + λ \nabla_{x_{t}} \log p (y ∣ x_{t}) \end{array}

局限：

分类器能分的类有限，泛化性不足
增加了计算成本
误差累计与非端到端

2.5.2 Classifier-free guidance

紧跟 OpenAI 之后，谷歌大脑团队发表了一篇论文 Classifier-free diffusion guidance。Classifier-free 只需要在 classifier guidance 基础上稍微变换一下即可。
我们希望消除 $\nabla_{x_{t}} \log p (y ∣ x_{t})$ ，那么由式子1，

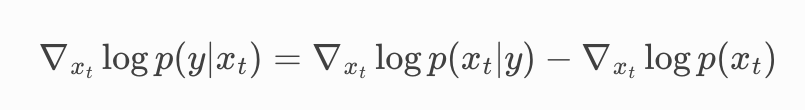
然后将其带入到式子2，

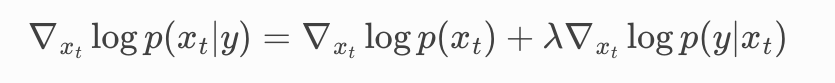
可得：

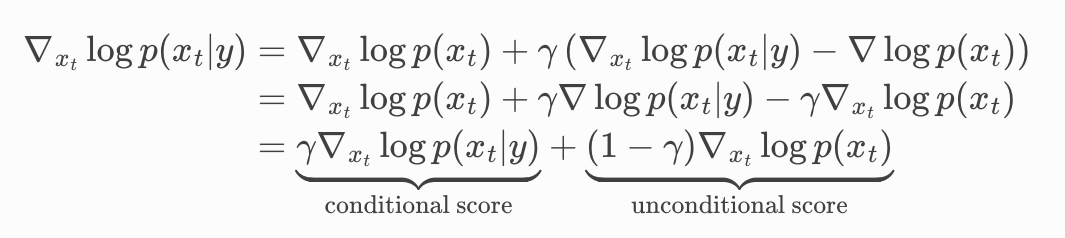
$\nabla_{x_{t}} \log p (x_{t} ∣ y)$ 这一项表明，本来的模型应该需要能处理这项工作

这样就消除了分类器梯度那一项。

Tips：

当你的主模型训练好之后，需要加入条件控制时，应该考虑classifier guidance方法

如果没有训练好，那么可以考虑Classifier-free guidance方法

2.5.3 直接加入相关控制信息

参数化模型有三种预测方案, 分别是

直接预测原始的 $x_{0}, {\hat{x}}_{θ} (x_{t}, t) \approx x_{0}$
预测噪声数据, ${\hat{ϵ}}_{θ} (x_{t}, t) \approx ϵ_{0}$
预测得分 (梯度), ${\hat{s}}_{θ} (x_{t}, t) \approx \nabla_{x_{t}} \log p (x_{t})$

最直觉（简单）的添加条件的方式, 就是和添加 $t$ 一样, 直接把 $y$ 作为模型的输入，添加到模型中即可，上面三种方式分别改成：

直接预测原始的 $x_{0}, {\hat{x}}_{θ} (x_{t}, t, y) \approx x_{0}$
预测噪声数据, ${\hat{ϵ}}_{θ} (x_{t}, t, y) \approx ϵ_{0}$
预测得分 $($ 梯度 $), {\hat{s}}_{θ} (x_{t}, t, y) \approx \nabla_{x_{t}} \log p (x_{t} ∣ y)$

2.5.3.1 Best Practice

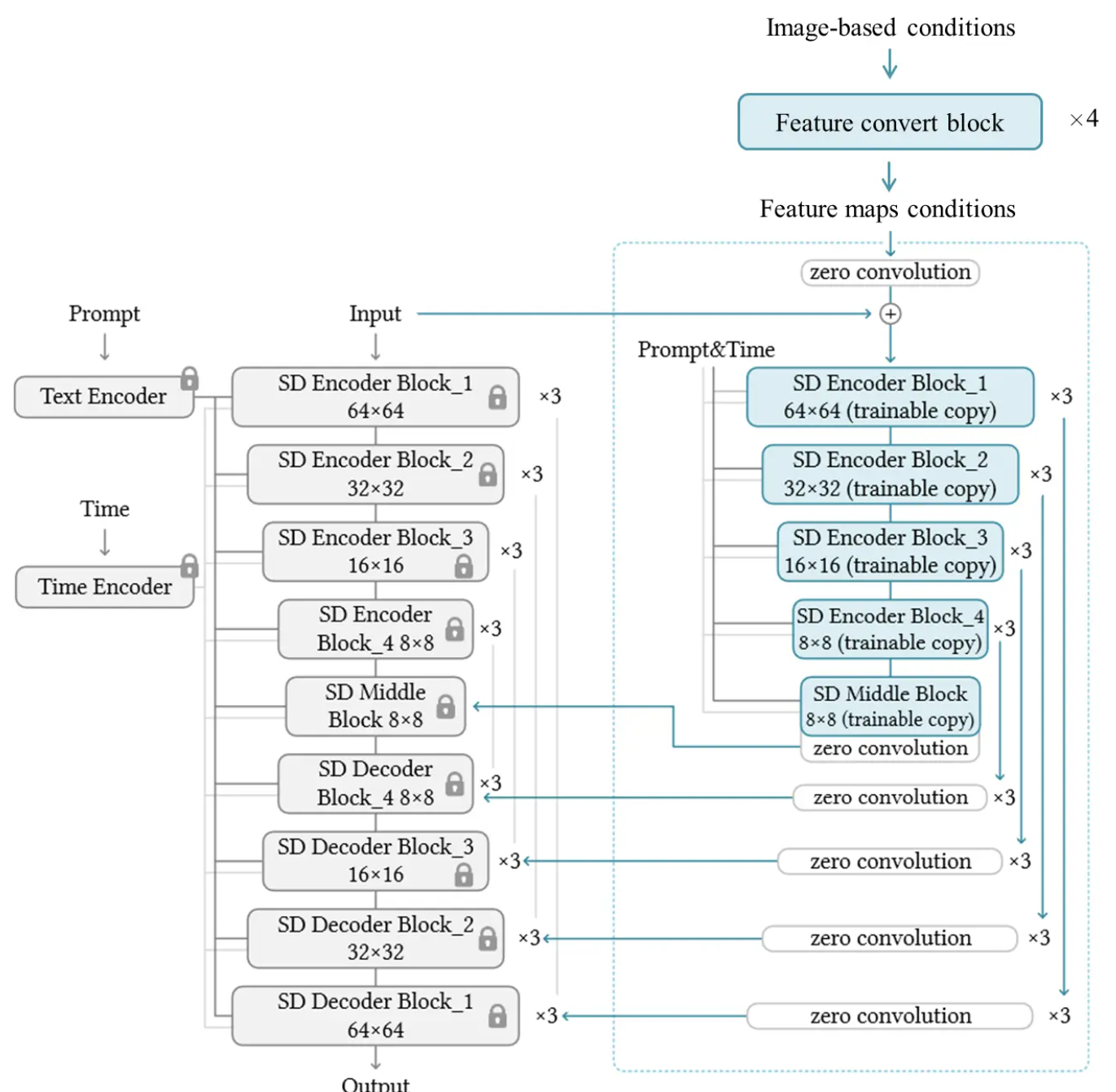
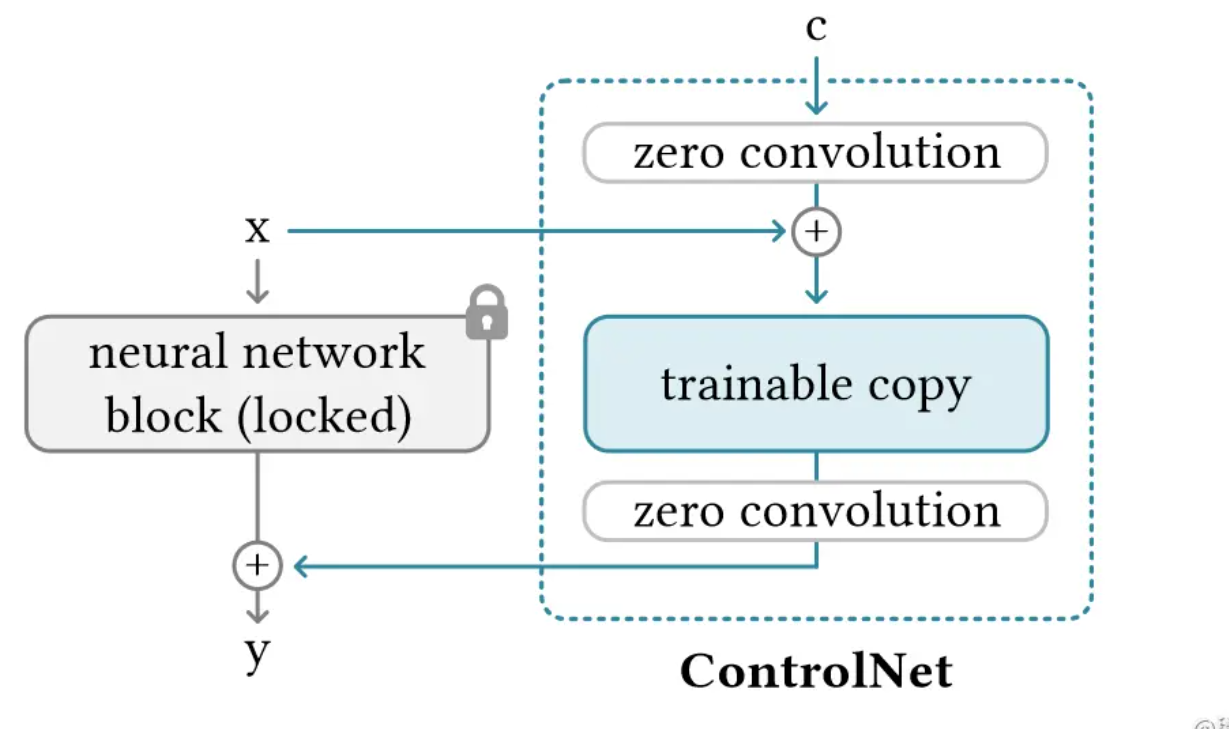
ControlNet(ICCV 23 Best Paper、23K star): 在文生图任务中表现出色的模型，特点是文本prompt控制和ControlNet图像条件控制。
不加入条件控制，只包含文本prompt控制的SD生成结果：

加入了条件控制的SD结果：

ControlNet同Lora，是一种外接训练层微调方式。其特点在于：将原始模型的编码器冻结并拷贝，用于条件的编码，然后将各层的条件编码与各层的原始编码，以UNet的U型结构，经Zero Convolution后进行残差连接，最后输出到解码器中。

模型简化图如下：

Zero Convolution可以看作是一种特殊的参数初始化方法，是一个1×1的卷积层，其所有权重（即卷积核的元素）和偏差在初始化时都被设置为零。
Zero Convolution初始时，不会给深度特征添加新的噪声，因此适合于，在保留原始模型权重的同时，对特定任务进行微调或训练。这或许有助于网络在训练初期保持稳定性，并可能促进更快的收敛。

3 补充

3.1 扩散模型如何能够学习到数据图像的固有偏差

扩散模型通过逐步添加噪声并再逐步移除噪声的过程，能够很好地捕捉图像数据的局部平滑性和多尺度结构，这与其工作机制和图像数据的特性密切相关。

以图像数据的局部平滑性和多尺度性进行举例说明。

3.1.1 局部平滑性 (Local Smoothness)

局部相关性：图像的一个基本特性是其局部区域的像素通常是相关的，也就是说，空间上接近的像素值通常变化平滑。这种局部平滑性是图像固有的特性。
扩散过程的作用：在逐步添加噪声的过程中，扩散模型逐步打破这种局部相关性，使图像逐渐变得平滑和模糊。这一过程让模型学习到如何从逐渐被破坏的局部结构中恢复出清晰的图像，从而捕捉到图像的局部平滑性。
去噪能力：在反向过程中，模型通过学习从噪声中逐步还原图像，可以更好地重建和保持局部平滑性，生成逼真的图像。

3.1.2 多尺度结构 (Multi-Scale Structure)

图像的多尺度特性：图像具有多尺度的特性，即同一个图像在不同的尺度上（从局部小结构到整体大结构）都有不同的信息层次。例如，图像中的纹理可能存在于细小的局部区域，而物体的轮廓和形状则体现在较大的尺度上。
逐步去噪的多尺度性：扩散模型通过逐步去噪的过程，在每个步骤中处理的尺度逐渐变大。最初的去噪步骤处理的是大范围的粗糙结构，而后面的步骤则逐渐恢复较小的细节。这种逐步的去噪方式自然地模拟了图像中的多尺度特性，使模型能够在不同的尺度上有效地重建图像结构。

1 简介

2 理论

2.1 马尔科夫链过程

2.1.1 详细推导

2.2 Score-Based Diffusion

2.2.1 背景

2.2.2 对比

2.2.3 分数函数

2.2.3.1 采样过程

2.2.3.2 训练目标函数

2.3 SDE与DDPM

2.4 Score-Based SDE Diffusion

2.4.1 内容

2.5 基于条件的扩散模型

2.5.1 classifier guidance

2.5.2 Classifier-free guidance

2.5.3 直接加入相关控制信息

2.5.3.1 Best Practice

3 补充

3.1 扩散模型如何能够学习到数据图像的固有偏差

3.1.1 局部平滑性 (Local Smoothness)

3.1.2 多尺度结构 (Multi-Scale Structure)

4 参考资料